110. Csoportkohomológia II. – Derivációk, kereszthomomorfizmusok, invariáns részmodulusok

2019. 01. 22

110. Csoportkohomológia II. – Derivációk, kereszthomomorfizmusok, invariáns részmodulusok

Filed under: Csoportkohomológia — 'n Quijote @ 19:20

A csoportkohomológiát tulajdonképpen csoporthatás-kohomológiának kéne nevezni, hiszen az nem egy csoportot, hanem egy csoporthatást vizsgál a homologikus algebra eszközeivel. A csoportkohomológia egy $G$ csoportnak egy $A$ Abel-csoporton való csoporthatásához rendel egy kolánc-komplexust, vagyis modulusok egy sorozatát a köztük ható kohatár-leképezésekkel. Ezt a kolánc-komplexust kétféleképpen szokás megválasztani, de a két kolánckomplexus izomorf egymással. Az “igazi” kolánc-komplexus egyszerű, viszont nagyon absztrakt és a megértéséhez a kategóriaelmélet és a homologikus algebra jó néhány fogalmának és összefüggésének az ismerete szükséges. A másik inkább technikai jellegű, a megértéséhez nem kell túlságosan sok előismeret, ellenben egy kicsit ad hoc jellegűnek tűnik. Kicsit olyan “fizikusos”. Mi most ez utóbbival kezdjük.

A csoportkohomológia alapszintű tárgyalása

Az alábbiakban definiálni fogjuk a csoporthatáshoz rendelt kolánc-komplexus első néhány modulusát, és a köztük ható kohatár-leképezéseket, amelyek meghatározzák, hogy a koláncok közül melyek a kociklusok, és melyek a kohatárok. A kociklusok és kohatárok hányadoscsoportja az adott rendű kohomológiacsoport.

Az itt leírtak főleg May – The cohomology of Groups cikkén, a Wikipedia Group cohomology szócikkén, és Weibel könyvén alapulnak.

Derivációk és kereszthomomorfizmusok

Korábban már volt róla szó, és most idézzük fel, hogy az algebra mint algebrai struktúra egy olyan vektortér, amelyben a vektorok nem csak összeadhatók, hanem szorozhatók is egymással, és a szorzat az összeadásra nézve balról is és jobbról is disztributív, ezen felül még ez a szorzás kompatibilis a skalárral való szorzással. Vagyis tetszőleges $x,y,z$ elemre és $a,b$ skalárra:

$(x+y)\cdot z=x\cdot z+y\cdot z$ (jobboldali disztributivitás)
$x\cdot (y+z)=x\cdot y+x\cdot z$ (baloldali disztributivitás)
$(ax\cdot b y) = (ab)(x\cdot y)$ (kompatibilitás)

Például az $n\times n$ -es (tehát négyzetes) valós mátrixok a valós számtest feletti algebrát alkotnak. Az algebra definíciója változtatás nélkül alkalmazható akkor is, ha egy $K$ test feletti vektortér helyett egy $R$ gyűrű feletti modulusra alkalmazzuk. Előbbi esetben a $K$ test feletti, utóbbiban az $R$ gyűrű feletti algebráról beszélünk, melyre példa az egész számokból álló $n\times n$ -es mátrixok mint az egész számok gyűrűje feletti algebra.

Egy algebrában tehát 3 művelet van: összeadás, egymással szorzás és skalárral való szorzás. Az összeadásra és a skalárral való szorzásra nézve az algebra vektortér, az összeadásra és az egymás közti szorzásra nézve pedig gyűrű. Az $n\times n$ -es mátrixokban ez a három művelet mind megvan, viszont $n\neq m$ esetén az $n\times m$ -esekben csak kettő, mert azok egymással nem szorozhatók össze. Tehát azok nem algebrát alkotnak, hanem csak vektorteret, vagy modulust. Viszont mivel balról szorozhatók az $n\times n$ -es mátrixokkal, ezért, ha most nem a valós számokat tekintjük skalároknak, hanem az $n\times n$ -es mátrixokat, akkor – mivel az $n\times n$ -es mátrixok gyűrűt alkotnak – az összeadással, és az $n\times n$ -es mátrixokkal való balról szorzással bal-modulust alkotnak. Ugyanígy, az $m\times m$ -es mátrixok gyűrűjét véve, azokkal pedig jobb-modulust. A kettővel együtt, padig egy $M_n(\mathbb R)-M_m(\mathbb R)$ , vagy $M_n(\mathbb Z)-M_m(\mathbb Z)$ bimodulust, ahol $M_n(\mathbb R)$ az $n\times n$ -es, $M_m(\mathbb R)$ pedig az $m\times m$ -es valós mátrixok gyűrűje, $M_n(\mathbb Z)$ illetve $M_n(\mathbb Z)$ pedig az egész számokból állóké. Ezzel el is mondtam, hogy mi az, hogy bimodulus: egy $R-S$ -bimodulus definíció szerint egy Abel-csoport, amely egyrészt az $R$ gyűrű feletti bal-modulus, másrészt pedig az $S$ gyűrű feletti jobb-modulus. A mátrixos példánkban az Abel-csoport az $n\times m$ -es mátrixok az összeadásra nézve, $R$ az $n\times n$ -es, $S$ pedig az $m\times m$ -es mátrixok gyűrűje. Persze az $n\times m$ -es valós mátrixokat tekinthetjük $\mathbb R-\mathbb R$ -bimodulusnak is, az egész számokból álló $n\times m$ -es mátrixokat pedig $\mathbb Z-\mathbb Z$ bimodulusnak is. Az $R-R$ bimodulusokat egyszerűbben az $R$ gyűrű feletti bimodulusnak nevezzük.

Tetszőleges $R$ gyűrű tekinthető egy önmaga feletti bimodulusnak is, ilyen értelemben a bimodulus a gyűrű fogalmának az általánosítása. Ez lehetőséget ad nekünk arra, hogy olyan definíciókat, amelyekben gyűrűk szerepelnek általánosíthassunk bimodulusokra. Ilyen fogalom például a deriváció. Egy $M$ differenciálható sokaságon értelmezett valós értékű, végtelen sokszor differenciálható függvények $C^\infty(M)$ halmaza a pontonkénti összeadással illetve egymással való szorzással gyűrűt alkot, így egyúttal saját maga feletti bimodulust is. A sokaságon egy $X$ vektormező egy $C^\infty(M)\to C^\infty(M): f\to X(f)$ leképezés, ahol $X(f)$ az $M\to\mathbb R: p\mapsto X_p(f)$ függvény. Erre a leképezésre érvényes a Leibniz-szabály, azaz $X(fg)=X(f)g+fX(g)$ . Ennek a fogalomnak az általánosítása az alábbi

definíció. Legyen $A$ egy $R$ gyűrű feletti bimodulus. Azokat a $D:R\mapsto A$ csoporthomomorfizmusokat, amelyek kielégítik a $D(rs)=D(r)s + rD(s)$ Leibniz-szabályt, derivációknak nevezzük.

A derivációkat bizonyos speciális esetben kereszthomomorfizmusoknak is nevezzük.^[1] A speciális eset az, amikor $R$ egy $\mathbb ZG$ csoportgyűrű, $A$ pedig egy bal- $\mathbb ZG$ -modulus (ami ekvivalens azzal, hogy $A$ egy $G$ -modulus), amit egy $\mathbb ZG$ bimodulusnak tekintünk úgy, hogy a $G$ jobboldali csoporthatását a triviális csoporthatásnak vesszük (tehát annak, ami $G$ minden eleméhez $A$ identitás-leképezését rendeli). A kereszthomomorfizmus definíciója tehát:

Definíció Legyen $G$ egy csoport, $A$ pedig egy $G$ -modulus, vagyis egy Abel-csoport, amin adva van a $G$ csoporthatása: $G\times A\to A: (g,a)\mapsto g\cdot a$ . Egy $D:G\to A$ leképezést a $G$ csoport $A$ -beli kereszthomomorfizmusának nevezzük, ha $D(g_1g_2) = D(g_1) + g_1\cdot D(g_2)$ .

Definíció. Legyen $G$ egy csoport, $A$ pedig egy $G$ -modulus. A $P_a:G\to A: g\mapsto g\cdot a - a$ . leképezést a $G$ csoportnak az $a$ elemhez tartozó $A$ -beli principális kereszthomomorfizmusának nevezzük.

Állítás. A principális kereszthomomorfizmus kereszthomomorfizmus.
Bizonyítás. $P(g_1) + g_1P_a(g_2)=(g_1\cdot a - a) + g_1\cdot(g_2\cdot a - a) = g_1g_2\cdot a - a = P_a(g_1g_2)$ .
$\Box$

Invariáns részmodulus és 0-kociklusok

Legyen $G$ egy csoport, $A$ pedig egy G-modulus. Az $A$ csoport műveletét additív módon írom, és pl. $a+b^{-1}$ -et $a-b$ -nak írom. A csoportkohomológia ehhez a G-modulushoz (vagyis $G$ -nek $A$ -n való csoporthatáshoz) egy kolánckomplexust rendel hozzá, amely – mint minden kolánckomplexus – modulusokból áll. Ennek a kolánckomplexusnak a modulusai közül a 0-koláncok $C^0(G,A)$ modulusa definíció szerint maga $A$ , az 1-koláncoké, $C^1(G,A)$ pedig a $G$ -ből $A$ -be ható összes függvények modulusa (a függvények közti modulus-műveleteket pontonként értelmezzük). A $d^1:C^0(G,A)\to C^1(G,A)$ kohatár-leképezés úgy van definiálva, hogy a 0-kociklusok $A$ -nak azok az elemei legyenek, amiken a csoporthatás triviális, vagyis, amelyeket $G$ minden eleme helyben hagy. Egy G-modulusnak azt a részmodulusát, amelyen $G$ csoporthatása triviális invariáns részmodulusnak nevezzük. A 0-kociklusok tehát $A$ invariáns részmodulusát alkotják, a továbbiakban ezt a részmodulust $A^G$ -vel jelölöm. Az, hogy az $a\in A$ elemet helyben hagyja a $g\in G$ csoportelem csoporthatása azt jelenti, hogy $g\cdot a = a$ . Ha tehát azt akarjuk, hogy $A^G$ elemei legyenek a kociklusok, akkor ezt a

$d^1:A\to C^1(G,A): a\mapsto P_a$

(1)

kohatár-leképezés megoldja, hiszen $P_a$ pontosan azokra az $a\in A$ elemekre 0, amelyekre tetszőleges $g\in G$ elemet véve $P_a(g) = g\cdot a - a = 0$ azaz, amelyekre $g\cdot a = a$ tetszőleges $g\in G$ esetén. Mint látjuk a $d^1$ leképezés az $a\in A$ elemhez a $G$ csoport $a$ elemhez tartozó $A$ -beli principális kereszthomomorfizmusát rendeli, ami tehát egy kereszthomomorfizmus, és $C^1(G,A)$ eleme. A 0-kociklusok a 0-kohatárú 0-koláncok. $A$ -ban egyetlen kohatár van, $A$ egységeleme (0). A 0. kohomológiacsoport definíció szerint a

$\displaystyle H^{0}(G,A)=\frac{\text{0-kociklusok}}{\text{0-kohat\'{a}rok}}=\frac{A^G}{\{0\}} = A^G$

(2)

modulus.

Kereszthomomorfizmusok mint 1-kociklusok

A kolánckomplexusunk következő modulusa, $C^2(G,A)$ definíció szerint a $G\times G\to A$ függvények modulusa. Mint már említettem az 1-koláncok modulusa, $C^1(G,A)$ a $G$ -ből $A$ -be ható összes függvények modulusa. Az (1) összefüggés szerint az 1-kohatárok ezek közül a principális kereszthomomorfizmusok. Kérdés, hogy mik az 1-kociklusok, vagyis mi a $C^1(G,A)\to C^2(G,A)$ kohatár-leképezés, amelynek a magja adja az 1-kociklusok részmodulusát. Nos, ez a kohatár-leképezés úgy van definiálva, hogy az 1-kociklusok pontosan a kereszthomomorfizmusok legyenek. A $d^2:C^1(G,A)\to C^2(G,A)$ kohatár-leképezés a $h\in C^1(G,A)$ függvényhez definíció szerint a

$d^2(h): G\times G\to A: (g_1,g_2)\mapsto h(g_1) + g_1\cdot h(g_2)- h \left (g_1 g_2 \right )$ .

(3)

függvényt rendeli. A kereszthomomorfizmus definíciójára rápillantva azonnal látszik, hogy ez pontosan akkor 0, ha $h$ kereszthomomorfizmus. A kohatár-leképezésre teljesülnie kell, hogy kohatár kohatára 0, tehát ha speciálisan $h$ kohatár, vagyis ha $h(g) = g\cdot a- a$ valamely $a\in A$ elemmel, akkor erre a függvényre a (3) kifejezés 0-t kell, hogy adjon. Ez láthatóan így is van, hiszen ekkor

$g_1\cdot h(g_2) - h \left (g_1 g_2 \right ) + h(g_1)= g_1\cdot(g_2\cdot m-m)- (g_1 g_2\cdot m - m ) + (g_1\cdot m - m)=0$ .

(4)

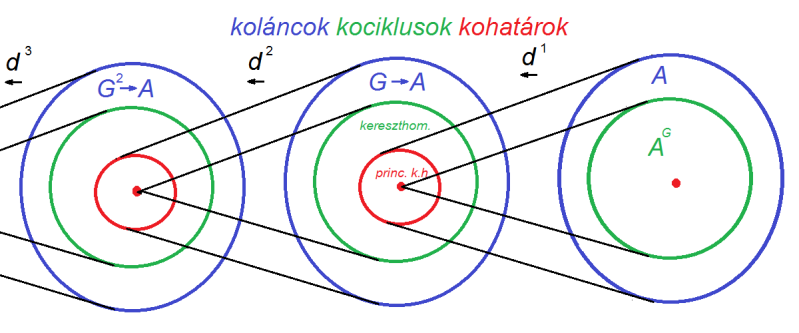
Összefoglalás

A $G$ csoport $A$ -n megvalósuló csoporthatáshoz tartozó kolánckomplexusunkból tehát eddig ennyit sikerült felderítenünk:

A kérdés most az, hogy

mik a $d^2$ leképezés értékkészletében lévő $G^2\to A$ függvények, vagyis mit írjunk a baloldali piros körbe
mi a $d^3$ kohatár-leképezés, vagyis mit írjunk a baloldali zöld körbe

Ezekkel a kérdésekkel folytatjuk majd a következő bejegyzésben.

^Ld. Weibel(1994), 174. old. 6.4.1. definíció

Comments (1)

1 hozzászólás »

[…] az esetben az csoporthatás -t G-modulussá teszi, ezért az előző bejegyzésben foglaltaknak megfelelően az függvényeket 1-koláncoknak, a függvényeket pedig 2-koláncoknak […]

Visszajelzés Szerző: 111. Csoportkohomológia III. – Csoportbővítések és a második kohomológiacsoport | Newton törvényeitől a Higgs-bozonig — 2019. 06. 28 @ 08:16 | Válasz

RSS feed for comments on this post. TrackBack URI

Hozzászólás Kilépés a válaszból

Ez az oldal az Akismet szolgáltatást használja a spam csökkentésére. Ismerje meg a hozzászólás adatainak feldolgozását .

Newton törvényeitől a Higgs-bozonig

2019. 01. 22